Modes of operation of block ciphers

Symmetric block ciphers encrypt messages of a certain length, which is specific to the chosen algorithm (e.g. 16 bytes for the AES algorithm, 8 bytes for the 3DES algorithm). These are called blocks. If the block is too short to be processed by the cryptographic algorithm, padding should be used. If the message is too long the solution will be to divide it into blocks of appropriate length. The mode of operation (mode of operation) of a block cipher are different techniques for combining blocks during an encryption operation. They are also called block cipher mode of operation or commonly referred to as encryption mode. In the following post, I will introduce two of them: electronic code book( ECB) mode and cipher block chaining( CBC) mode. Both modes are described in FIPS 81.

Electronic code book

Electronic codebook mode encryption involves independent encryption of each block. This is also where the name of this mode comes from. A codebook is a collection of certain phrases and their corresponding phrases after encryption (in this case, encryption). If for a given key (and we encrypt blocks from a message with the same key) we create all possible plaintexts and cryptograms corresponding to them we will get a codebook. There will be as many codebooks as possible keys for a given cipher. To encrypt using a given codebook, it is necessary to find the corresponding plaintext and the corresponding cryptogram. The decryption operation will proceed similarly.

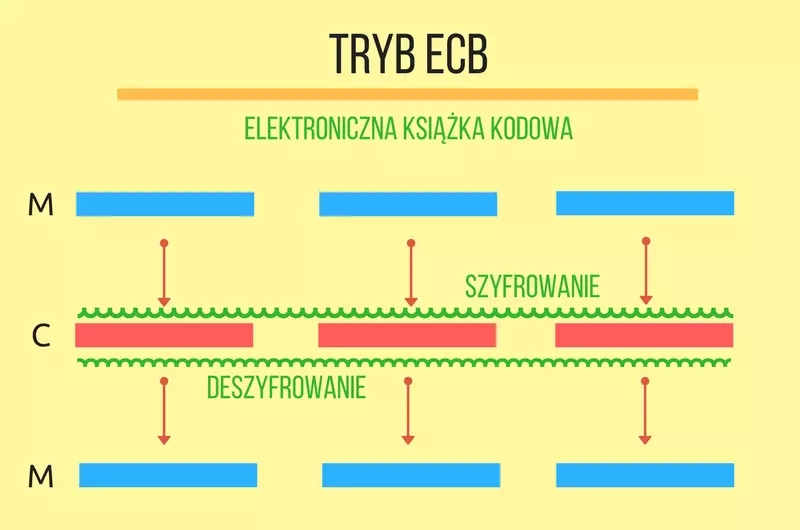
The following example encrypts and decrypts two blocks of data in ECB mode. I encourage you to complete it with a code snippet that prints out the plaintext and cryptogram on the screen and take a look at the results. You can use the printHexBinary(byte[] val) method of the javax.xml.bind.DatatypeConverter class.

1import javax.crypto.Cipher;
2import javax.crypto.spec.SecretKeySpec;
3
4public class ECBTest {
5    public static void main(String[] args) throws Exception {
6        byte[] plain = "abcdefghijklmnopabcdefghijklmnop".getBytes();
7        byte[] key = "klucz--128-bitow".getBytes();
8
9        SecretKeySpec secretKey = new SecretKeySpec(key, "AES");
10        Cipher cipher = Cipher.getInstance("AES/ECB/NoPadding");
11
12        // szyfrowanie
13        cipher.init(Cipher.ENCRYPT_MODE, secretKey);
14        byte encrypted[] = cipher.doFinal(plain);
15
16        // deszyfrowanie
17        cipher.init(Cipher.DECRYPT_MODE, secretKey);
18        byte decrypted[] = cipher.doFinal(encrypted);
19    }
20}

If we encrypt identical blocks with the same key twice, we get two identical ciphertexts. This is consistent with the idea of a codebook. Of course, the attacker does not know what the plaintext was, but he already knows that the same block was encrypted twice. If his knowledge of the construction of the plaintext is greater, he can easily use the transmitted ciphertexts to attack. However, he will not try to decrypt them and will only manipulate their order. Let's assume that the amount of the transfer is transmitted in the form encrypted with the AES algorithm as 32 digits (2 blocks of 16 bytes each). It is much more likely that the significant digits are in the second block than in the first, since as a rule transfers are not made for such large amounts. The attacker is not able to decrypt the cryptograms, but he can swap them in places. He will gain even more if he removes the first cryptogram and replaces it with the second. The receiving system will decrypt the data correctly (it will be digits), but the amount is likely to be significantly higher. The attacker by manipulating the cryptogram has made a successful attack. It is also very important that using a secure algorithm (AES) in an unsafe way (bad mode of operation) we got an unsafe system! It is worth trying to make such an attack yourself by modifying the example program.

Another good example is the image of this penguin, the confidentiality of which is hard to talk about after encryption in ECB mode. A given color in an unclassified picture after encryption became a different color, but always the same.

Do the above examples clearly indicate that this mode is dangerous and should not be used at all? In my opinion, not always. It all depends on what applications it is used in and whether we are aware of what attacks it can lead to. A much more serious mistake than the use of ECB mode in the first attack example was the failure to ensure authentication of the data source.

The security problem of ECB mode can be looked at in yet another way. Using the reasoning from the previous article related to the black box, we can imagine an ECB cipher inside it. Can an attacker easily distinguish it from a random number generator by sending messages and observing the responses? Maybe. I leave it to the readers to find sample queries to such a black box enabling them to effectively distinguish it from a random number generator.

Binding of ciphertext blocks

The mode of operation with the binding of ciphertext blocks*(binding of encrypted blocks*) eliminates the basic disadvantages of the electronic codebook mode by creating a relationship between individual blocks using xor operations. Before encryption, a block undergoes an xor operation with the previous cryptogram. The same operation is performed after decryption which makes it possible to recover the plaintext, since double xor with the same data removes the transformation before encryption restoring the original plaintext. The first block does not have a preceding cryptogram so the xor operation is performed with a so-called initialization vector ( IV), also known as the initialization vector.

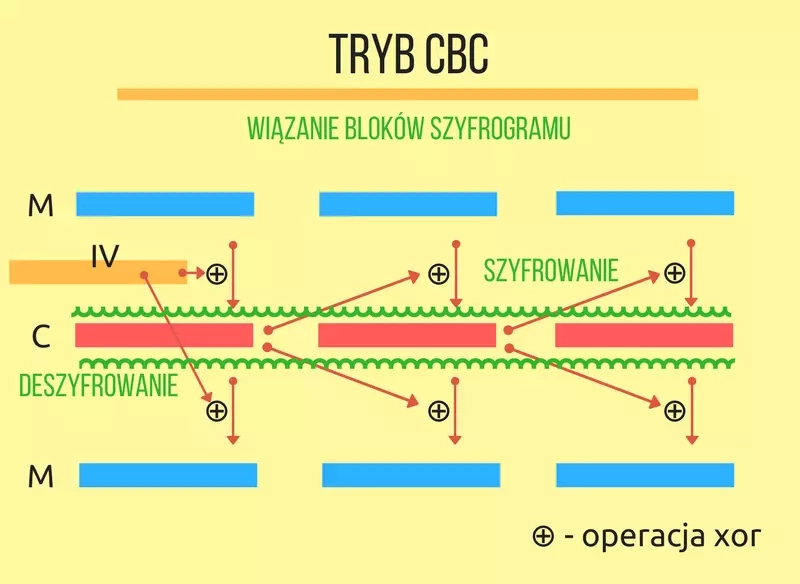
The program previously used for encryption in ECB mode will require several modifications. In addition to changing the mode, a parameter representing the initialization vector will be necessary. An instance of the IvParameterSpec class contains it. Again, I encourage you to complete the code with a snippet that prints the plaintext and cryptogram on the screen and take a look at the results.

1import javax.crypto.Cipher;
2import javax.crypto.spec.SecretKeySpec;
3import javax.crypto.spec.IvParameterSpec;
4
5public class CBCTest {
6    public static void main(String[] args) throws Exception {
7        byte[] plain = "abcdefghijklmnopabcdefghijklmnop".getBytes();
8        byte[] key = "klucz--128-bitow".getBytes();
9        byte[] iv = "-blok-wektor-iv-".getBytes();
10
11        SecretKeySpec secretKey = new SecretKeySpec(key, "AES");
12	IvParameterSpec ivps = new IvParameterSpec(iv);
13        Cipher cipher = Cipher.getInstance("AES/CBC/NoPadding");
14
15        // szyfrowanie
16        cipher.init(Cipher.ENCRYPT_MODE, secretKey, ivps);
17        byte encrypted[] = cipher.doFinal(plain);
18
19        // deszyfrowanie
20        cipher.init(Cipher.DECRYPT_MODE, secretKey, ivps);
21        byte decrypted[] = cipher.doFinal(encrypted);
22    }
23}

What should the initial vector be? Considering the black box experiment: if the initial vector is predictable or even the same every time (and this often happens in running systems), you can easily get rid of it by properly preparing the first block. Before encryption, we perform xor with the predicted initial vector. The mode will perform a second xor removing the changes made by the IV. This will encrypt the first block in its original value, without the influence of the initialization vector. Therefore, the initial vector should be random (which in cryptography implies the assumption of its uniqueness). There is no contraindication for the initial vector to be passed in an explicit form. It can be treated as an unused part of the cryptogram (the initialization vectors of subsequent blocks are the preceding cryptograms that we transmit in the unprotected channel).

So, modifying the above example, instead of initializing vector IV with the same data, one would have to use random data there:

1byte[] iv = new byte[16];
2        new SecureRandom().nextBytes(iv);

After such a change, the cryptogram will look different each time. Penguin, which was mentioned earlier, encrypted in CBC mode may look like this picture. It is already fully hidden.

Apart from these advantages, does the CBC mode have any disadvantages? Unfortunately, yes. While it is not possible to manipulate the plaintext at will through modifications in the cryptogram, it is easy to remove its beginning (by removing the beginning of the cryptogram and substituting a start vector) or its end (by removing the end of the cryptogram). This can be avoided by sending the length of the entire original message in the cryptogram. Each time, it is necessary to keep in mind the aforementioned randomness of the initialization vector.

Summary

Block cipher modes of operation are used when you are encrypting more than a single block of data. The right choice of mode can be crucial for security, as we have seen with some simple examples. It should be noted that the two modes of operation presented do not ensure the integrity and authentication of the transmitted data. Of course, they could be supplemented with an independently calculated MAC. There are modes that are designed with these essential services in mind. These are the so-called block cipher modes of operation for implementing authenticated encryption( AE) and authenticated ecnryption with additional data ( AEAD), in which authentication of the transmitted encrypted and plaintext data is also provided. Block cipher modes of operation are plentiful, and many of them, along with security analyses and current recommendations, are listed on the NIST website.