I will present some machine learning algorithms that are now often used to build models. Since the target audience is managers, my goal is not to describe precisely how an algorithm works. Instead, I will give some intuitions to understand why some algorithms may be better than others, why it is worth trying different ones, and why we may not be able to use any of them in a particular problem.
Linear and logistic regression
One of the oldest approaches to model building is linear regression. It was used by statisticians long before the term "machine learning" appeared. Suppose our goal is to understand how a person's height depends on the height of his mother, father and gender. Perhaps this relationship could be described by the following formula:
height = 40 + 0.3 * mother's height +0.4 *father's height + 15 * gender
How could we use such a formula? Let's assume that in a certain family a son was born, his mother is 170 cm tall, his father is 180 cm tall. Let's base these values in the formula, assuming that we denote the son by 1, the daughter by 0. We will get the following result:
height = 40 + 0.3 * 170 + 0.4 * 180 + 15 * 1 = 178
Such a formula is a certain model (not necessarily right), thanks to which we are able to make a prediction of future values. But not only that: we can understand how the various variables (predictors) are related to height. If the mother was 1 cm taller, the child should be 0.3 cm taller on average, on the other hand, if a daughter was born, she would be 15 cm shorter (because we would substitute 0 for gender). That is, the model can also be used for inference.
Linear regression is an algorithm that finds the coefficients (parameters, weights) given in the formula above (40; 0.3; 0.4; 15). Its essence is the assumption that the considered relationship is linear, that is, it is enough to multiply the values of the predictors by the corresponding numbers and add them. The reality may be far from this assumption.
We will use linear regression only in regression problems, that is, when we predict a quantitative variable. Logistic regression, on the other hand, is most simply looked at as a modification of linear regression, by which we solve a classification problem. The important thing is that in this approach, too, we rely on the assumption of linearity.
When is it worth using regression? If our main goal is to understand the relationship between (Y) and (X) (inference), then a model in which the form of this relationship is clearly visible --- and this is what regression has. However, it should be remembered that the relationship under consideration does not have to be linear at all. However, by modifying the predictors in an appropriate way, we are able to model non-linear relationships as well.
Decision tree
We can describe the relationship between height and the other variables using conditional sentences, for example:
- If a girl is born whose mother is above 170 cm, she will be 168 cm. 2) If a girl is born whose mother is below 170 cm, she will be 164 cm. 3) If a boy is born whose father is above 182 cm, he will be 180 cm. 4) If a boy is born whose father is below 182 cm, he will be 176 cm.
Such sentences can be represented in the form of a tree, as below.
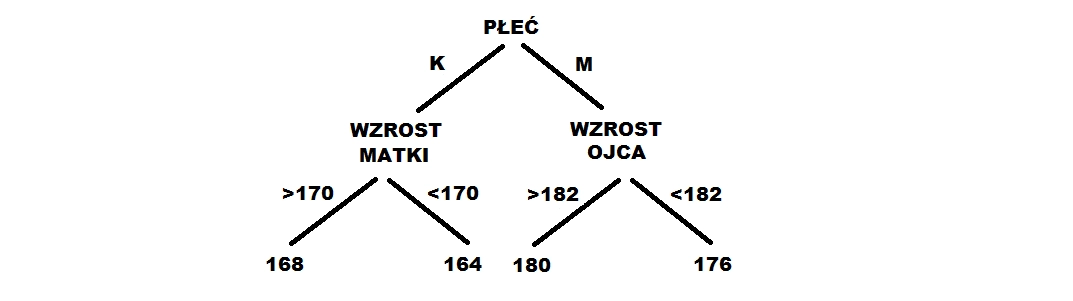
A decision tree is an algorithm that finds such conditional sentences, or more precisely: the best dividing points (> 170 cm, < 170 cm), the right order of variables (gender first) and the right values (168, 164) with which we can predict someone's height.
When might we want to use this approach? Trees assume virtually nothing about the nature of relationships between variables, and are flexible. They are easily able to model so-called interactions when the relationship between variables is influenced by other variables (for example, the relationship with a father's height may be different for men and women). In the case of regression, this effect can also be achieved, but it has to be explicitly introduced into the model (we have to assume in advance that the interaction will occur). In addition, when the tree is not too long, it can be easily used for inference.
Random Forest, Extreme Gradient Boosting
Although trees are flexible and can describe complex relationships, in practice they are often imprecise. Note, for example, that in the previous example we use only four different values for prediction: 164, 168, 176, 180. Of course, the tree can be longer and then there will be more of these values. Nevertheless, such a single tree is usually not the best model. It turns out that a very good solution is to build multiple trees on slightly modified data (in a nutshell). Each of them determines a forecast, and then they are somehow combined into one (for example, by averaging). Importantly, such a final model ceases to be a tree and there is no way to easily interpret it.
Approaches to how to combine multiple trees are numerous. Currently, some of the most popular are Random Forest and Extreme Gradient Boosting. The differences between the two are difficult to explain simply, but from a manager's point of view they don't matter much. The important thing is that both algorithms are capable of detecting very complex relationships and in practice often prove to be the most accurate. However, it should be remembered that they are a kind of black box and it is not entirely clear why they make such and not other predictions. They are also usually very elaborate and their implementation in the final product can cause some problems.
Neural network
Neural networks are currently marketing very well. Admittedly, in many issues related to artificial intelligence, it is indeed possible to obtain very good results with their help, but unless your business goal is to identify lesions on an X-ray or to build a self-driving car, a network is probably not the best choice.
It is easiest to look at a neural network as a generalization of regression. The main difference is that the algorithm, in a sense, is able to find suitable predictors on its own, which can be helpful in predicting the feature of interest. This is particularly important in problems such as image recognition, where it is not easy to indicate what such predictors might look like.
The network can easily be expanded to enormous size, obtaining a very complex model that has virtually nothing to do with regression anymore. Importantly, however, it usually takes many observations to do this --- perhaps too many for us to use in our problem.
Which model will work in my situation?
First, we need to consider whether the problem we want to solve is regression or classification. In the former we can use all the given algorithms except logistic regression, in the latter all but linear regression. Further, we should determine what we care more about: on understanding the phenomenon or forecasting new cases? If the former is more important, we need a model from which we can draw as many reliable conclusions as possible. A good choice might be a regression or a decision tree. If, on the other hand, the focus is on forecasting, there is a good chance that a random forest or Extreme Gradient Boosting will prove better.
Can we then say in advance that a particular algorithm will be the best? No. The standard in model building is to test various approaches, from very simple to very complex (as long as we have enough observations for the latter). Even if we are interested in forecasting, the nature of the phenomenon may be such that an accretive regression will turn out to be the best. On the other hand, even though we would like to understand a relationship, it may be so complex (or we don't have access to the right predictors) that regression will only mislead us. The whole point is that until we start building a model, we often don't know what kind of relationship to expect.
If you want to know more about machine learning, be sure to read our previous articles:
- Machine learning for managers
- What is a machine learning model? - A guide for managers
- How to find the best machine learning model?
Also check out our training courses in the Data Science category.




